Виды задающих и возмущающих воздействий.
Возмущения, действующие на САР, представляют собой непрерывные функции времени с различными законами изменения. Часто такой же характер имеют задающие воздействия. Поэтому поведение САР в реальных условиях представляет собой сочетание переходного и установившегося режимов. В этом случае возникают трудности принципиального характера, т.к. заранее неизвестны законы измерения внешних воздействий, что затрудняет анализ динамики и статики САР, Для ликвидации возникших затруднений часто используют так называемые типовые, управляющие и возмущающие воздействия, которые представляют собой либо наиболее вероятные, либо наиболее неблагоприятные законы изменения управляющих и возмущающих воздействий. Например, довольно широко в качестве типовых используют воздействия полиномиального вида: (1.1)
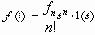
где n= 0,1,2 … натуральные числа;

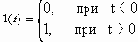
1(t) называется единичная ступенчатая функция.
При n=0 выражение (1.1) определяет ступенчатое воздействие: (1.2)
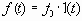
При n=1 из выражения (1.1) получим линейное воздействие ( воздействие с постоянной скоростью): (1.3)
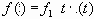
При n=2 из выражения (1.1) получим воздействие с постоянным ускорением: (1.4)
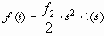
Графическое представление типовых воздействий, соответствующих уравнениям (1.2), (1.3), (1.4) представлено на рис. 1.6.
В некоторых случаях в качестве типового используется воздействие следующего вида:
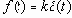
где d (t) – единичная дельта-функция
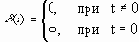
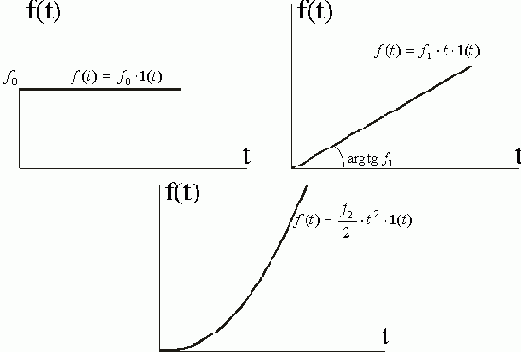
Рис 1.6. Типовые полиномиальные воздействия
Единичная дельта - функция (единичный импульс) представляет собой математическую идеализацию импульса бесконечно малой длительности, бесконечно большой амплитуды, имеющего конечную площадь, равную единицы, т.е:
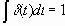
Существует следующая связь между единичной ступенчатой функцией и дельта – функцией:
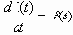
Кроме того, часто применяются гармонические типовые воздействия:
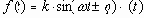
где k- постоянный коэффициент; w - частота; j -фаза.
Момент приложения внешних воздействий к САР обычно принимается за нуль отсчёта времени. При таком подходе внешние воздействия для отрицательного момента времени равны нулю. В связи о этим, в аналитические выражения для внешних воздействий в качестве множителя вводят единичную ступенчатую функцию.
Любое внешнее воздействие сложной формы может быть приближенно представлено в виде совокупности типовых воздействий, связанных между собой определенными математическими операциями.