Типовые звенья и их характеристики
В общем случае какой-либо объект в теории автоматического управления описывается передаточной функцией, содержащей полиномы от р произвольного порядка в числителе и знаменателе. Но если передаточная функция объекта содержит только простой множитель в числителе (знаменатель при этом представляет собой действительное число) либо только простой множитель в знаменателе (числитель представляет собой действительное число), то объект называется типовым динамическим звеном (или просто типовым звеном).
Из курса алгебры известно, что полином любого порядка можно разложить на простые множители. То есть любую САУ можно представить в виде последовательного соединения типовых звеньев. С другой стороны, реальные звенья САУ могут иметь самую разнообразную физическую основу (электронные, механические, гидравлические, электромеханические и т.п.) и конструктивное выполнение, но иметь одинаковые передаточные функции и являться одинаковыми типовыми звеньями. Поэтому знание характеристик звеньев столь же необходимо для расчетов САУ, как знание таблицы умножения в арифметике.
Все линейные типовые звенья разделяют на три группы: позиционные звенья, интегрирующие и дифференцирующие. Позиционные звенья: апериодическое, пропорциональное, колебательное, консервативное и чистого запаздывания - характеризуется тем, что в каждом из них, кроме консервативного, при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины.
В звеньях, относящихся к группе интегрирующих, при постоянном входном воздействии выходная величина неограниченно растет.
Дифференцирующие звенья характеризуются тем, что реагируют только на изменение входной величины.
Рассмотрим типовые звенья и их характеристики.
Пропорциональное (безинерционное) звено
. Описывается уравнением и имеет передаточную функцию:
xвых(t)=kxвх(t),W(p)=k.
Параметр k называется в общем случае коэффициентом передачи звена и может иметь любую размерность. В частных случаях, когда k является величиной безразмерной, принято пользоваться термином "коэффициент усиления".
Частные и временные функции звена:
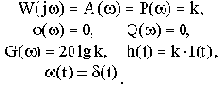
Примерами таких звеньев могут служить механические связи, электронные усилители сигналов на низких частотах и др.
Схема на рис.2.6, б, если Z1(p)=R1 и Zoc(p)=Roc, также будет являться пропорциональным звеном.
Интегрирующее (идеальное) звено.
Уравнение и передаточная функция звена:
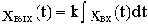
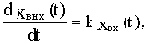
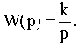
В случае интегрирующего звена параметр k является коэффициентом передачи звена по скорости, численно равным скорости изменения выходной величины при единичном значении входной величины.
Частотные и временные функции звена:
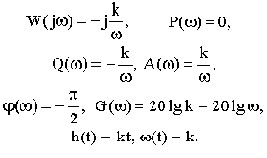
Построенные по указанным функциям характеристики звена представлены на рис.2.12.
При построении ЛАЧХ удобно отложить точку с координатами
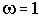
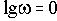
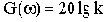
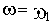
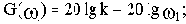
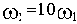
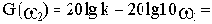
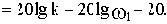
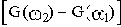
В качестве примера элемента, характеристики которого приближенно соответствуют характеристикам идеального интегрирующего звена, можно назвать двигатель постоянного тока с независимым возбуждением и малой электромеханической инерцией. Входной величиной для него является напряжение на зажимах якоря, а выходной - угол поворота вала.
Схема на рис.2.6, б будет являться интегрирующим звеном, если Z1(p)=R1, а цепь обратной связи организована конденсатором, т.е.
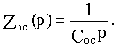
На самом деле, согласно формуле (2.5) передаточная функция схемы будет
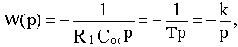
где k=1/T=1/(R1Coc).
При использовании в рассматриваемой схеме реального операционного усилителя переходная характеристика не может иметь значения, превышающие напряжение питания . Но если предположить операционный усилитель идеальным, то и реализованное здесь интегрирующее звено будет идеальным.
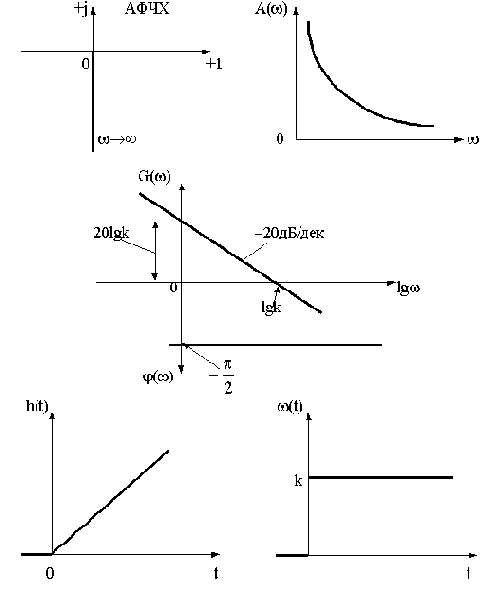
Рис.2.12
Дифференцирующее (идеальное) звено.
Уравнение и передаточная функции звена:
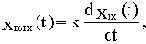
Выходная величина пропорциональна скорости изменения входной величины.
Если входная и выходная величины имеют одинаковую размерность, то коэффициент k измеряется в секундах. В этом случае его принято обозначать через Т и называть постоянной времени дифференцирующего звена.
Выражение для основных функций:
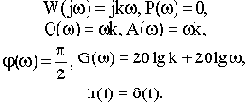
Как передаточная функция, так соответственно и частотные характеристики дифференцирующего звена обратны передаточной функции и соответствующим характеристикам интегрирующего звена.
О том, что звено с представленным математическим описанием является идеальным, говорит, к примеру, переходная функция. Ни в каком реальном устройстве невозможно получить скачек выходной величины бесконечной амплитуды.
Реальные дифференцирующие звенья обладают конечной инерционностью, вследствии чего осуществляемое ими дифференцирование не является точным. Примером может служить тахогенератор, если за его входную величину принять угол поворота его вала, а за выходную величину - выходное напряжение. Последнее пропорционально угловой скорости вращения вала, которая в свою очередь равна производной от угла поворота.
Логарифмические частотные характеристики рассматриваемого звена приведены на рис.2.13.
При построении ЛАЧХ удобно отложить точку с координатами
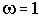
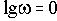
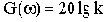
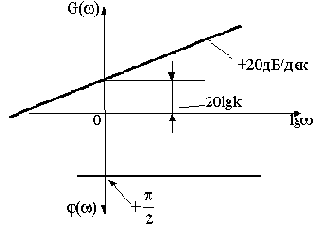
Рис.2.13
Апериодическое (первого порядка) звено.
Описывается дифференциальным уравнением
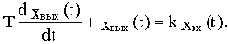
Перейдя к изображениям, получим:
TpXвых(p)+Xвых(p)=kXвх(p)
Передаточные и частотные функции:
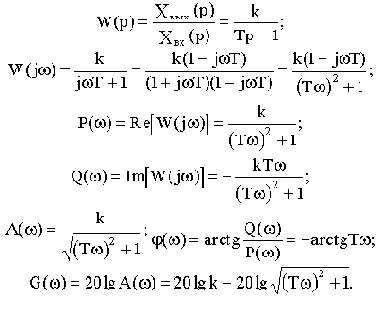
ЛАЧХ звена показана на рис.2.14. Но эта же характеристика может быть представлена приближенно ломаной линией, которая показана на том же рисунке. Эта приближенная характеристика называется асимптотической ЛАЧХ. Такое название связано с тем, что эта характеристика составлена из двух асимптот, к которым стремится ЛАЧХ при


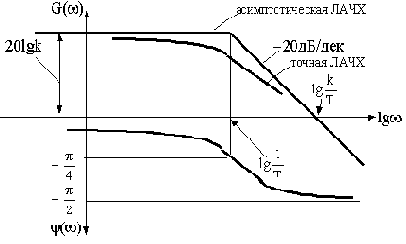
Рис.2.14
При малых значениях

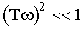
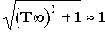
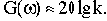
Соответственно характеристика представляет собой прямую, параллельную оси абсцисс и проходящую на уровне 20lgk. Это есть первая асимптота, к которой стремится ЛАЧХ при

С другой стороны, на больших частотах
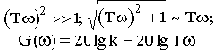
В этом случае характеристика представляет собой прямую, имеющую наклон минус 20 дБ/дек. Действительно, при увеличении

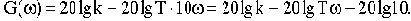
Таким образом, величина
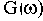

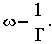
Максимальное расхождение между точной (GТ) и асимптотической (Ga) ЛАЧХ наблюдается при частоте, равной сопрягающей.
Вычислим это расхождение, подставив в соотношения для GT и Ga значения сопрягающей частоты
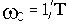
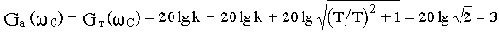
От параметров звена рассматриваемая величина не зависит.
На этом же рисунке показана и ЛФЧХ: при



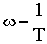
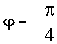
АФЧХ представляет собой полуокружность с радиусом


Переходная функция, согласно решению уравнения звена, при xвх=1(t) и нулевых начальных условиях имеет вид
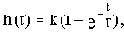
а импульсная переходная функция
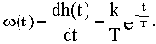
Переходная характеристика представлена на рис.2.15.
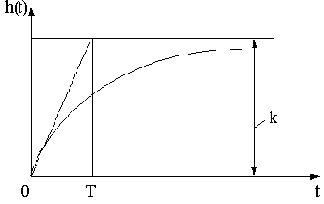
Рис.2.15
Динамические свойства звена характеризуются постоянной времени Т. Постоянная времени может быть определена как время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени.
Коэффициент передачи k определяет свойства звена в установившемся режиме.
Очевидно, имея в распоряжении частотные либо переходные характеристики, полученные, например, экспериментально, можно восстановить передаточную функцию звена.
В рассмотренных выше примерах по определению передаточных функций схемы на рис.2.2; рис.2.3; рис.2.6, а являются апериодическими звеньями.
Пример 2.6.
Асимптотическая ЛАЧХ апериодического звена имеет частоту среза
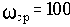
Нужно на графике или мысленно провести из точки на оси частот
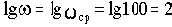
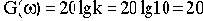
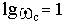
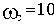
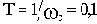
Звенья второго порядка.
В общем случае описываются уравнением
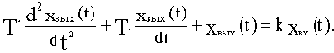
Перейдем к изображениям по Лапласу:
(T2p2+T1p+1)Xвых(p)=kXвх(p).
Отсюда определяем передаточную функцию:
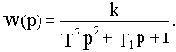
Однако общепринята запись передаточной функции звеньев второго порядка в другом виде:
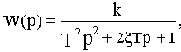
где
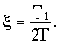
Звенья второго порядка, таким образом, характеризуются тремя параметрами. Это коэффициент передачи. постоянная времени и коэффициент демпфирования




Рассмотрим свойства колебательного звена. Выражения для его частотных функций имеют следующий вид:
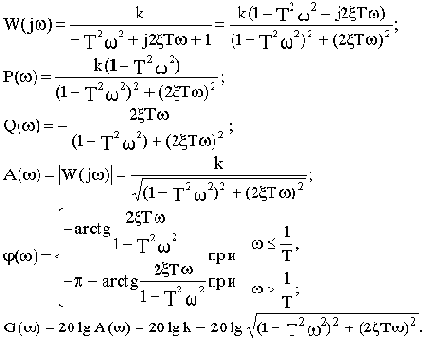
Асимптотическая ЛАЧХ строится тем же приемом, что и для апериодического звена. В области низких частот


G(

В области высоких частот
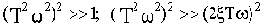


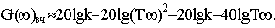
Эта асимптота имеет наклон минус 40 дБ/дек. Сопрягаются асимптоты на частоте
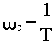
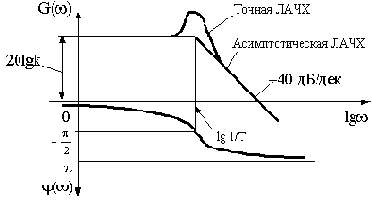
Рис.2.16
Точная ЛАЧХ GT несколько отличается от асимптотической Ga. Максимальная ошибка - в районе около сопрягающей частоты. Для упрощенных расчетов можно считать, что наибольшая ошибка будет при
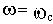
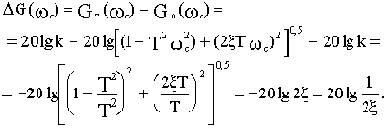
В районе

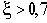
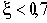
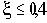
Представление о динамических свойствах звена можно получить из переходной характеристики, представленной на рис.2.17.
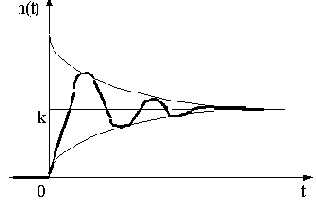
Рис.2.17
Примером звена второго порядка может служить колебательный контур (см. схему на рис.2.5 и вывод передаточной функции в примере 2.4).
Консервативное звено - частный случай колебательного звена, когда отсутствует демпфирование. Если обратиться к приведенному выше примеру (см. рис.2.5), то должны отсутствовать потери в контуре (выполняться условие R=0). В этом случае колебания стали бы незатухающими и переходная характеристика описывалась бы выражением:
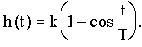
На сопрягающей частоте ЛАЧХ консервативного звена имеет всплеск бесконечной амплитуды, т.е. претерпевает разрыв, а ЛФЧХ из нулевого значения скачком достигает значения минус

При

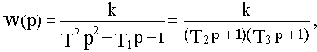
где
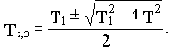
То есть апериодическое звено второго порядка не является типовым или элементарным, так как его можно представить двумя последовательно соединенными более простыми звеньями - апериодическими первого порядка.
Пример 2.7.
Определить, при каком соотношении параметров элементов схемы колебательный контур (см. рис.2.5) является колебательным звеном.
Запишем полученную в примере 2.4 передаточную функцию с использованием коэффициента демпфирования:
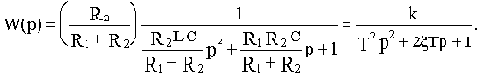
Отсюда выразим коэффициент демпфирования:
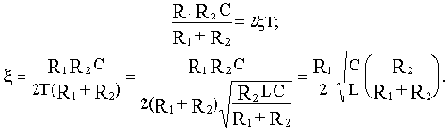
Звено будет колебательным, если

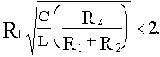
В противном случае, т.е. при
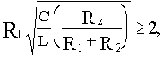
контур будет являться апериодическим звеном второго порядка. При этом следует обратить внимание на то, что лишь с позиций математического описания схему можно представить как последовательное соединение двух апериодических звеньев первого порядка. Расчленить же принципиальную схему на два участка, каждый из которых был бы соответствующим апериодическим звеном первого порядка, невозможно.
Звено чистого запаздывания.
Это звено без искажения воспроизводит на выходе входную величину, как идеальное пропорциональное звено, но с той разницей, что выходная величина запаздывает относительно входной на постоянное время. Уравнение такого звена имеет вид:
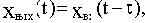
где

Очевидно, характеристики этого звена будут:
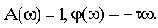
Отсюда АФЧХ:
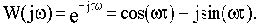
Передаточная функция:
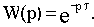
В качестве примера звена можно назвать длинную электрическую линию без потерь, механический транспортер и т.д.
По существу это звено относится к нелинейным. Однако при расчетах САУ с такими звеньями можно применять методы теории линейных систем. Поэтому часто элементы, закон движения которых мало изучен или трудно представим в аналитической форме, после некоторой идеализации представляются в виде звеньев запаздывания.
К содержанию