Структурные схемы и их преобразование
В теории автоматического управления под структурной схемой понимается графическое изображение математического описания. То есть для составления структурной схемы система дробится на элементы, каждый из которых описывается простейшим математическим выражением ( в виде передаточной функции). Структурные схемы содержат следующие четыре типа элементов: звенья направленного действия; устройства сравнения, или сумматоры; линии связи; точки разветвления (узлы).
Звенья направленного действия изображаются прямоугольниками, внутри которых записываются их передаточные функции.
Между собой звенья соединяются с помощью линий связи. На этих линиях стрелками указывается направление распространения сигналов. Следует подчеркнуть, что в направлениях, противоположных указанным стрелками, сигналы не распространяются. Сами линии связи, также как и сумматоры, считаются идеальными, то есть никакими параметрами не обладают.
Сумматоры предназначены для суммирования сигналов (с учетом знака сигнала), как и на функциональных схемах.
Для распределения сигналов по различным направлениям используются узлы, которые обозначаются точками в местах пересечения линий связи.
Для удобства расчетов бывает необходимо преобразовать исходную структурную схему системы к какому-либо желаемому виду, чаще всего - к цепи последовательно соединенных звеньев. В связи с этим рассмотрим основные правила преобразования структурных схем.
При последовательном соединении n звеньев с передаточными функциями Wi(p) эквивалентная передаточная функция Wэ(p) определяется их произведением:
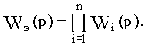
При параллельном соединении n звеньев эквивалентная передаточная функция определяется суммой передаточных функций Wi(p) отдельных звеньев:
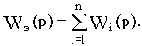
Для случая обратной связи при выводе эквивалентной передаточной функции замкнутого участка Wз(p) используем обозначения, приведенные на рис.2.8.
Схема замкнутого участка системы
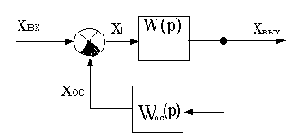
Рис.2.8
Обратная связь называется отрицательной, если
x1=xвх-xoc,
как показано на схеме, и положительно, если
x1=xвх+xoc.
В случае отрицательной обратной связи в изображениях по Лапласу с учетом указанных направлений распространения сигналов запишем:
Xвых(p)=X1(p)W1(p)=[Xвх(p)-Xoc(p)]W(p)=
[Xвх(p)-Xвых(p)Woc(p)]W(p).
Отсюда получаем передаточную функцию
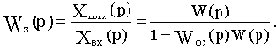
Для положительной обратной связи в знаменателе формулы знак "плюс" меняется на "минус".
Указанные три вида преобразования структурных схем являются наиболее часто встречающимися. Для остальных случаев сформулируем основной принцип преобразования и поясним несколькими примерами. При преобразовании структурной схемы передача сигнала по выбранному направлению не должна меняться.
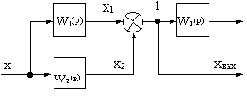
Например, в структурной схеме на рис.2.9, а необходимо перенести узел через звено с передаточной функцией W2(p).
Преобразование структурной схемы
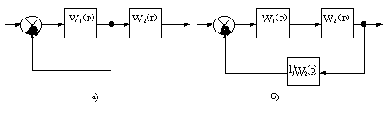
Рис.2.9
Чтобы передача сигнала по цепи обратной связи не изменилась, необходимо ввести фиктивное звено с передаточной функцией 1/W2(p), как показано на рис.2.9, б.
В более сложных случаях в процессе преобразования необходимо производить определенные расчеты.
Например, в схеме на рис.2.10, а узел 1 необходимо перенести на выход звена с передаточной функцией W2(p).
Преобразование структурной схемы
а)
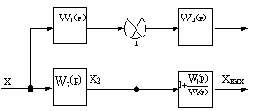
б)
Рис.2.10
Установим связь между величинами Xвых(p) и X2(p).
На входе звеньев с передаточными функциями W1(p) и W2(p) действует сигнал
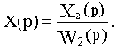
На выходе звена с передаточной функцией W1(p)
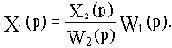
На выходе сумматора в узле 1
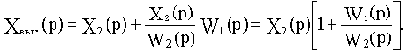
Отсюда видно, что в рассматриваемом примере при переносе узла необходимо ввести фиктивное звено с передаточной функцией
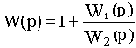
При переносе узла в схеме на рис.2.11, а с выхода сумматора на его положительный вход найдем передаточную функцию фиктивного звена без дополнительных пояснений.
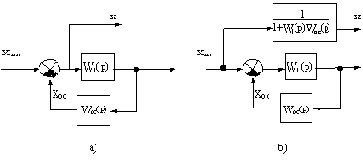
Рис.2.11
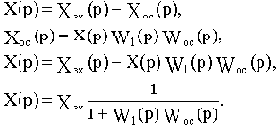
К содержанию