Критерий устойчивости михайлова

Основан также на рассмотрении характеристического полинома.

Подставим в этот полином вместо р мнимую переменную

. Получим комплексную функцию

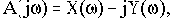
где

- действительная часть, полученная из членов А(р), содержащих четные степени р;

- мнимая часть, полученная из членов А(р) с нечетными степенями р.

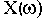
Изобразим А(

) в виде графика в комплексной плоскости, как показано на рис.3.6.

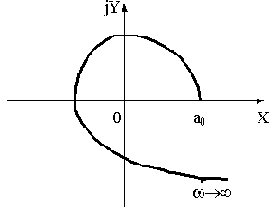
Рис.3.6

Этот график принято называть годографом Михайлова. Каждому значению

соответствуют определенные значения Х( ) и Y( ) и определенная точка на плоскости. При =0 функция А( )=а0, т.е. годограф начинается на действительной оси. При функция А( ) тоже неограниченно возрастает.

Сформулируем критерий Михайлова: система устойчива, если годограф А(

), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n - порядок системы.

Представленный выше годограф (см. рис.3.6) соответствует устойчивой САУ четвертого порядка.

Годограф Михайлова можно строить по точкам, изменяя частоту от нуля до бесконечности с определенным шагом и вычисляя каждый раз значение А(

).

Можно поступить по другому: найти точки пересечения годографа с осями и соединить их плавной линией. Для этого, определив из уравнения Х(

)=0 значения частот, соответствующих точкам пересечения годографа А() с мнимой осью, подставляют их в выражение Y(). В результате получают соответствующие координаты. Аналогично находят точки пресечения А() с действительной осью, приравнивая нулю мнимую часть Y().

Собственно, после того, как найдены значения

, при которых годограф А() пересекает оси координат, то есть нули Х() и Y(), нет необходимости строить сам годограф.

Из формулировки критерия следует, что устойчивость имеет место, если нули Х(

) и Y() чередуются с ростом , начиная с =0, когда Y()=0, а Х()>0.

Выше отмечалось, что условием нахождения САУ на границе устойчивости является попадание корня характеристического уравнения на мнимую ось плоскости корней. Но если характеристическое уравнение А(р)=0 имеет корень

, то удовлетворяется равенство

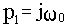
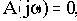
откуда получаем



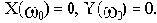
Графически это означает попадание одной точки годографа Михайлова в начало координат.

Таким образом. условием нахождения САУ на границе устойчивости является прохождение годографа Михайлова через начало координат (при какой-то частоте . Физический смысл величины - частота колебаний системы на границе устойчивости).

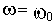
Но для нахождения на границе устойчивости должен быть пропущен лишь один квадрант. Другими словами, очертание кривой Михайлова на границе устойчивости должно быть таким, чтобы малой деформацией ее в начале координат можно было удовлетворить критерию Михайлова. Так, график на рис.3.7, а соответствует нахождению САУ на границе устойчивости, а график на рис.3.7, б - неустойчивости.



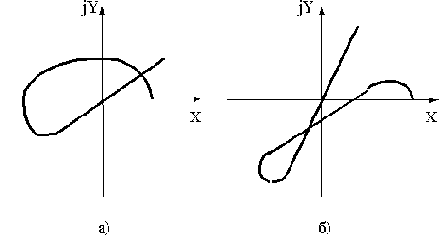
Рис.3.7

В качестве примера определим граничное значение коэффициента передачи kгр для рассмотренной выше САУ (см. рис.3.3).

Запишем функцию для построения годографа Михайлова, подставив в характеристический полином (3.4) вместо р мнимую переменную :



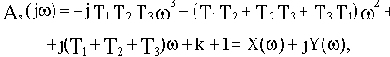
где

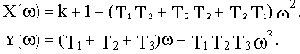
При нахождении САУ на колебательной границе устойчивости годограф Михайлова проходит через начало координат при частоте Поэтому при k=kгр:



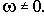
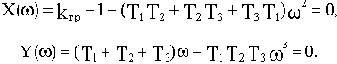
Из второго уравнения находим значение квадрата частоты, при котором годограф проходит через начало координат:



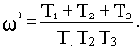
Подставив это значение в первое уравнение, получим



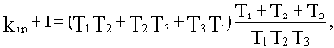
или окончательно



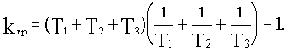
Получили, естественно, тот же результат, что и по критерию Гурвица.

Критерий Михайлова широко используется для построения областей устойчивости. Уравнения границы устойчивости в пространстве двух варьируемых параметров и , согласно этому критерию, имеют вид:



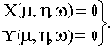
Исключив из этих уравнений параметр , можно получить уравнение границы устойчивости, связывающее входящие в выражения и варьируемые параметры и . Для определенности такой метод определения границы устойчивости будем называть “по критерию Михайлова”.

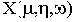
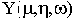
Собственно, так мы и поступили в только что рассмотренном примере.

С другой стороны, можно построить границы устойчивости по приведенной системе уравнений, используя как параметр, который изменяют от 0 до . Каждому значению при этом соответствует определенная точка границы устойчивости. Этот метод получения границы устойчивости принято называть методом D - разбиения.



Пусть характеристическое уравнение САУ в общем виде будет следующее:



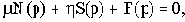
где N(p),S(p),F(p)- полиномы от р.

После подстановки получим:



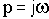
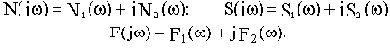
Исходное характеристическое уравнение распадается на два:

(3.6)

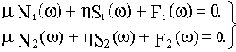
Решим эту систему уравнений:

(3.7)

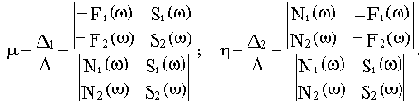
Построенный по выражениям (3.7) график называется кривой D - разбиения плоскости (,). При движении по кривой D - разбиения в сторону возрастания штриховку наносят слева, если определитель положителен, и справа - если отрицателен.

В результате получают область. которая может претендовать на область устойчивости. В заключение произвольную точку этой области проверяют любым из критериев устойчивости.

Пример 3.2.

Решить задачу примера 3.1 с использованием критерия Михайлова.

Подставим в выражение характеристического полинома вместо р комплексную переменную :



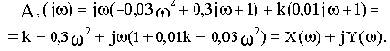
Для определения устойчивости не будем строить годограф Михайлова, а рассчитаем величину kгр, т.е. поступим аналогично примеру 3.1.

Условие нахождения САУ на границе устойчивости:



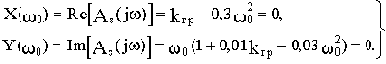
Корень второго уравнения отбрасываем, т.к. для нахождения системы на границе устойчивости годограф Михайлова должен пройти через начало координат при .

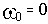
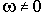
Тогда из второго уравнения определяем



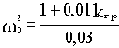
и подставляем в первое:



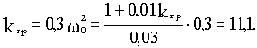
Получили тот же результат, что и в примере 3.1.

Пример 3.3.

По критерию устойчивости Михайлова определить устойчивость САУ по заданному характеристическому полиному:

A(p)=3*10-4p5+5*10-3p4+0,1p3+0,5p2+0,9p+1

Годограф Михайлова построим примерно, определив координаты пересечения его с осями координат.



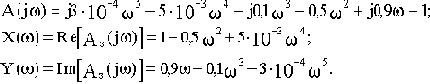
С учетом того, что годограф Михайлова строится при изменении от 0 до + , определим положительные корни уравнения X()=0: и неотрицательные корни уравнения Y()=0:

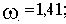
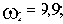
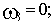
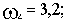
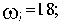
Координаты пересечения годографа Михайлова с осями координат (в порядке возрастания частоты):

1) Y=0; X=1;

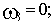
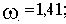
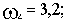
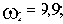
2) X=0; Y=0,9*1,41-0,1*1,413+0,0003*1,415=0,99;

3) Y=0; X=1-0,5*3,22+0,005*3,24=3,6;

4) X=0; Y=0,9*9,9-0,1*9,93+0,0003*9,95=-59,59;

5) Y=0; X=1-0,5*182+0,005*184=364.

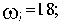
Примерный вид годографа Михайлова для полученных данных показан на рис.3.8. Исследуемая система устойчива.





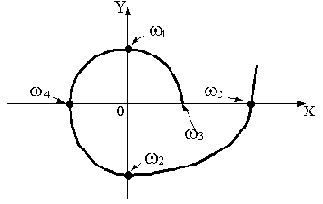
Рис.3.8

Пример 3.4.

Для САУ, структурная схема которой приведена на рис.3.3, определить область устойчивости методом D- разбиения. Варьируемые параметры T3 и k3. Значения неварьируемых параметров:

T1=0,1; T2=1; k1=2; k2=5.

Характеристический полином замкнутой САУ:

Aз(p)=(T1p+1)(T2p+1)(T3p+1)+k1k2k3=T1T2T3p3+

+(T1T2+T2T3+T3T1)p2+(T1+T2+T3)p+k1k2k3+1.

Представим последнее выражение в следующем виде:

Aз(p)=T3N(p)+k3S(p)+F(p).

Aз(p)=T3[T1T2p3+(T1+T2)p2+p]+k3(k1k2)+

+[T1T2p2+(T1+T2)p+1].

Сделаем подстановку :



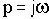
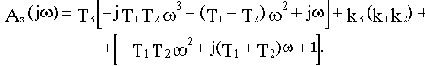
Выделим вещественную и мнимую части. представив их в следующем виде:



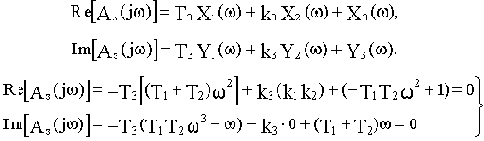
Рассчитаем для последней системы уравнений определители и :



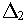
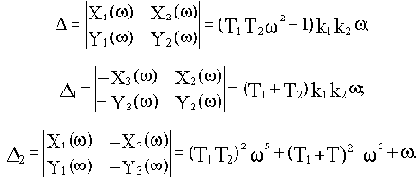
Найдем выражения для T3 и k3:



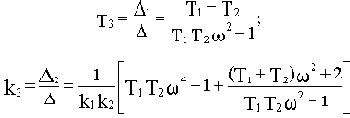
Подставляя численные значения, получим:



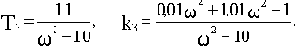
Результаты расчетов границы области устойчивости по последним выражениям сведены в таблицу. Еще две границы получаются в результате приравнивания нулю коэффициента характеристического полинома при p3 (T3=0) и свободного члена характеристического полинома:

k1k2k3+1=0,

k3=-1.

Область устойчивости построена на рис.3.9.

Таблица



0

1

2

3

4

5

7

10

15

20

Т3

-1,1

-1,2

-1,83

-11

1,83

0,73

0,28

0,12

0,051

0,028

k3

-0,1

-0,22

-0,86

-10,9

3,29

2,17

1,91

2,24

3,42

5,14



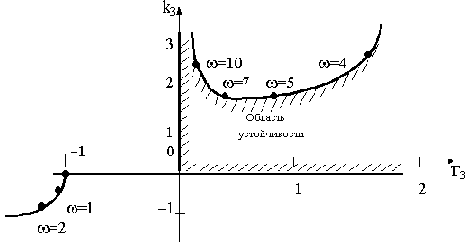
Рис.3.9

 К содержанию


Содержание раздела

---

---