Критерии качества переходного процесса

Исчерпывающее представление о качестве переходного процесса дает, естественно, сама кривая процесса. Однако при разработке САУ необходимо иметь возможность судить об основных показателях качества переходного процесса без построения их кривых, по каким-либо косвенным признакам, которые определяются более просто и, кроме того, позволяют связать показатели качества непосредственно со значениями параметров САУ. Такие косвенные признаки называются критериями качества переходного процесса.

Существуют три группы критериев качества: частотные, корневые и интегральные.

Наибольшее распространение получили частотные критерии, в основу которых положено использование частотных характеристик. Для иллюстрации возможности оценки качества переходного процесса по частотным характеристикам установим точную аналитическую зависимость между переходной характеристикой h(t) и вещественной частотной характеристикой (ВЧХ) P(

).

На основании возможности разложения функции времени в ряд Фурье единичное ступенчатое воздействие можно представить в виде выражения

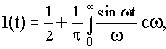
то есть суммы постоянной составляющей и бесконечного числа синусоид частотой

и амплитудой при изменении от 0 до .

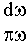
Уравнение АФЧХ имеет вид:

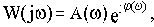
где

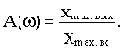
Если на вход системы подать 1(t), то каждому из входных синусоидальных колебаний

будет соответствовать колебание на выходе [с амплитудой , сдвинутое по фазе относительно входного колебания на угол () ]

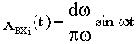
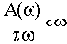
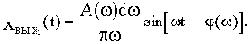
Постоянной составляющей

на входе будет соответствовать постоянная составляющая на выходе.

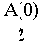
Результирующее значение выходной величины:

(4.3)

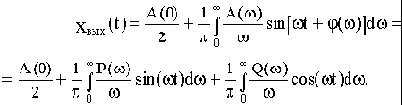
Так как воздействие 1(t) подается в момент t=0, то при t<0:

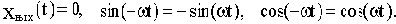
Уравнение (4.3) при подстановке значения (-t) вместо t примет вид:

(4.4)

Вычтем из уравнения (4.3) уравнение (4.4):

(4.5)

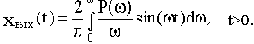
Пользуясь зависимостью (4.5), можно составить предварительное приближенное суждение о качестве переходной характеристики по виду ВЧХ. Различные типы ВЧХ представлены на рис.4.5.

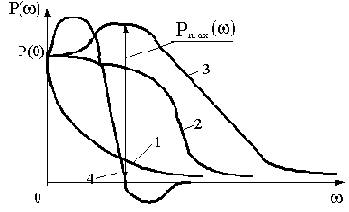
Рис.4.5

Основные положения оценки качества по ВЧХ сводятся к следующему:

1) приблизительно одинаковым частотным характеристикам соответствуют приблизительно одинаковые переходные характеристики;

2) значение переходной характеристики h(t) в установившемся состоянии подчиняется следующему соотношению



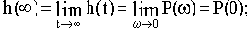
3) если ВЧХ имеет вид кривой 1 (см. рис.4.5), переходная характеристика будет монотонной;

4) для ВЧХ, имеющей вид кривой 2, характерно наличие перерегулирования у переходной характеристики величиной 18%;

5) наличие экстремума ВЧХ (кривая 3) увеличивает колебательность до величины



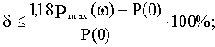
6) наличие экстремума ВЧХ в отрицательной области (кривая 4) проводит к дополнительному росту колебательности;

7) длительность переходного процесса tп оценивается приблизительно по величине интервала существенных частот cщ (в этом интервале Р() 0,05 Р(0), причем



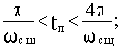
8) острый пик ВЧХ при свидетельствует о медленно затухающих колебаниях с чатотой, близкой к ;

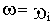
9) если при некоторой частоте ВЧХ претерпевает разрыв, то САУ является неустойчивой.

Колебательность переходной характеристики можно оценить по величине относительного максимума амплитудной частотной характеристики А(), примерный вид которой представлен на рис.4.6.



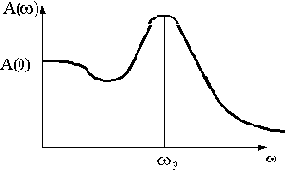
Рис.4.6

Величина относительного максимума называется показателем колебательности М и определяется отношением



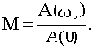
При М<1 переходная характеристика неколебательна. Чем больше М, тем больше колебательность. При М - незатухающие колебания. Оптимальным обычно считается М=1,3-1,5. При этом переходная характеристика имеет слабую колебательность с частотой, близкой к .

Вследствие предельной простоты построения ЛАЧХ удобно пользоваться именно этой характеристикой. Информацию здесь несет среднечастотная часть характеристики. При частоте среза наклон ЛАЧХ должен составлять минус 20 дБ/дек, а значение определяется временем переходного процесса tп и перерегулированием :



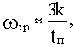
где k берется по графику на рис.4.7 в зависимости от величины .

Сопрягающие частоты ЛАЧХ слева и справа от , как показано на рис.4.8, рассчитываются по выражениям:



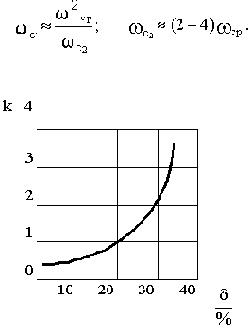
Рис.4.7



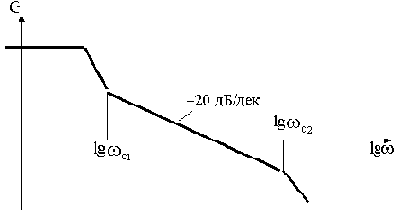
Рис.4.8



Величины наклонов ЛАЧХ слева от и справа от на качество переходного процесса почти не влияют.

Группа корневых критериев основана на оценке качества переходного процесса по значениям полюсов и нулей передаточной функции САУ.

Заметим, что при исследовании устойчивости нас интересовали лишь полюсы, здесь же необходимо учитывать и нули. Только в частном случае, когда нулей нет, качество переходного процесса определяется только полюсами. Начнем рассмотрение именно с такого случая.

Переходной процесс в устойчивой системе распадается на затухающие и колебательные составляющие. Если найти длительность самой длительной составляющей и величину колебательности самой колебательной составляющей, то по ним можно оценить верхние пределы величин длительности и колебательности всего переходного процесса.

Время затухания отдельной составляющей определяется величиной

,

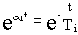
где - действительная часть i-го корня характеристического уравне-

ния,

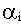
- постоянная времени затухания.

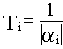
Можно считать, что длительность i-ой составляющей переходного процесса , то есть длительность составляющих переходного процесса обратно пропорциональна абсолютному значению действительной части корней характеристического уравнения.

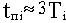
Абсолютная величина называется степенью устойчивости и обозначается .

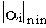
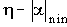
При этом длительность переходного процесса будет



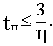
Термин “степень устойчивости” связан с тем, что геометрически - есть расстояние от мнимой оси, являющейся границей устойчивости, до ближайшего корня (см. рис.3.1).

Колебательность колебательной составляющей переходного процесса определяется отношением соседних максимумов:



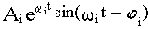
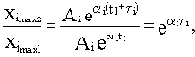
где t1- момент появления первого максимума i-й составляющей пере-

ходной характеристики,

- период колебаний данной составляющей.

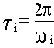
Таким образом, колебательность равна



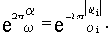
Следовательно, мерой колебательности является отношение : чем оно больше, тем больше колебательность составляющей. Наиболее колебательной является составляющая, у которой это отношение максимально. Соответствующая величина обозначается и называется степенью колебательности.



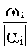
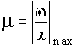
В комплексной плоскости корень, определяющий наиболее колебательную составляющую, соответствует наибольшему значению угла между лучом, направленным через корень из начала координат, и действительной отрицательной полуосью.

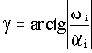
Далее отметим влияние на качество переходного процесса наличия нулей передаточной функции. Положительные члены полинома числителя передаточной функции приведут к повышению колебательности и убыстрению переходного процесса, а отрицательные - к затягиванию переходного процесса.

Интегральными критериями

качества называются такие, которые одним числом оценивают и величины отклонений, и время затухания переходного процесса. Для пояснения используем рис.4.9.



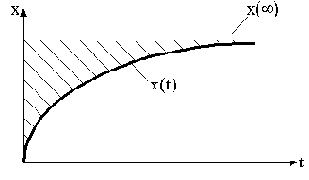
Рис.4.9

Обозначим отклонение выходной величины от нового установившегося значения

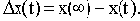
Для монотонного процесса интегральной оценкой может служить заштрихованная площадь над кривой переходного процесса (см. рис.4.9), то есть



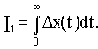
Интеграл I1 называется линейной интегральной оценкой. Процесс будет тем лучше, чем меньше число I1.

Однако такая оценка не годится для колебательного процесса, так как площади, расположенные ниже и выше прямой х(), будут иметь разные знаки. Поэтому по минимуму величины I1 наилучшим оказался бы процесс с незатухающими колебаниями.

В связи с этим в общем случае принимают квадратичную интегральную оценку качества в виде



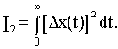
Целесообразность применения интегральных критериев заключается в том, что в литературе имеются формулы, выражающие I2 (или другие интегральные оценки) непосредственно через коэффициенты дифференциального уравнения САУ.

Интегральные критерии качества используются для определения оптимальных значений варьируемых параметров по минимуму значения соответствующей интегральной оценки.

Применяются интегральные критерии обычно в теории оптимальных систем.

 К содержанию


Содержание раздела

---

---