Частотные характеристики

Если на вход линейной непрерывной системы (или отдельного звена) подать синусоидальные (гармонические) колебания с постоянными амплитудой и частотной

, то после затухания переходных процессов на выходе также возникают синусоидальные колебания с той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний. Как известно из курса "Основы теории цепей, часть 1", синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд. Комплексные амплитуды рассматриваемых здесь входных и выходных колебаний можно записать как и

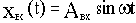
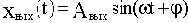
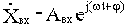
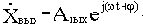
Подавая на вход системы гармонические колебания с постоянной амплитудой, но различными частотами, на выходе системы тоже получаем гармонические колебания с теми же частотами, но различными амплитудами и фазами относительно входных колебаний.

Введем в рассмотрение отношение комплексных амплитуд выходных и входных колебаний:

(2.6)

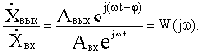
Функция

называется комплексной частотной и получается чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции переменной р на переменную :

(2.7)

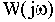
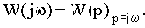
В различных формах записи функцию

можно представить в следующем виде:

(2.8)

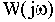
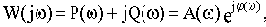
где

и - действительная и мнимая части комплексной частотной функции,

и - модуль и аргумент комплексной частотной функции.

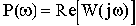
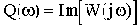
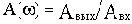
При фиксированном значении частоты

комплексную частотную функцию можно изобразить вектором на комплексной плоскости, как показано на рис.2.7.

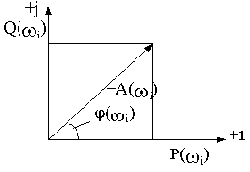
Рис.2.7

Изменение частоты приведет к изменению величины и расположения вектора на комплексной плоскости, а конец вектора опишет некоторую траекторию. Геометрическое место концов векторов комплексной частотной функции при изменении частоты от нуля до бесконечности называется амплитудно-фазовой частотной характеристикой (АФЧХ).

В свою очередь все величины, представленные в (2.8), являются соответствующими частотными функциями, а построенные по выражениям для функций графики - частотными характеристиками.

называется вещественной частотной, а - мнимой частотной характеристикой.

показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется амплитудной частотной характеристикой.

показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется фазовой частотной характеристикой.

Между всеми частотными характеристиками существует непосредственная связь, вытекающая из тригонометрических соотношений и поясняемая рис.2.7.



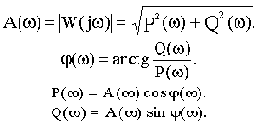
В практических расчетах чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе, что позволяет в значительной степени сократить объем вычислительных работ.

Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство при выражении десятичным логарифмом величины отношения мощности на входе Pвых к мощности на входе Pвх в технике принят бел. Так как мощность сигнала пропорциональна его амплитуде, получим:



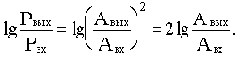
Но так как бел является достаточно крупной единицей усиления (ослабления) мощности (увеличению мощности в 10 раз соответствует 1 Б), то за единицу измерения ее принят децибел 1дБ=0,1 Б.

С учетом этого можно записать:



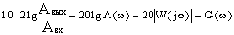
Величина логарифма амплитудной частотной характеристики, выраженная в децибелах

xвх(t)=1(t)

называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ).

Таким образом, изменению отношения двух амплитуд в 10 раз соответствует изменение усиления на 20 дБ, в 100 раз - на 40 дБ, в 1000 раз - на 60 дБ и т.д.

Вычислим, какому отношению амплитуд соответствует один децибел, два и т.д.

1дБ=20lg(Aвых/Aвх);

lg(Aвых/Aвх)=1/20;



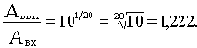
То есть 1 дБ 1,222.

2 дБ ~ (1,222)2=1,259;

3 дБ ~ (1,222)3=1,259;

4 дБ ~ 1,585;

5 дБ ~ 1,778;

6 дБ ~ 1,995 2.

Фазовая частотная характеристика , построенная в полулогарифмическом масштабе (в координатах: угол в градусах или радианах и ), называется логарифмической фазовой частотной характеристикой (ЛФЧХ).

За единицу измерения частоты используется логарифмическая единица декада. Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением.



В логарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную



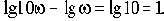
ЛАЧХ и ЛФЧХ строят обычно совместно, используя общую ось абсцисс (ось частот). Начало координат невозможно взять в точке , так как . Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот.

Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза . Ось абсцисс соответствует значению , то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства).

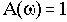
Из рассмотренных здесь частотных характеристик две можно получить экспериментально-амплитудную и фазовую Woc(p). Из этих двух экспериментальных остальные частотные характеристики могут быть рассчитаны по соответствующим формулам, например - по формуле (2.8). Кроме того, рассчитав по экспериментальным данным , по (2.7) путем обратной подстановки (заменив на р) можно получить передаточную функцию, по (2.4) - из передаточной функции дифференциальное уравнение в операторной форме и далее, применив обратное преобразование Лапласа - дифференциальное уравнение (уравнение динамики системы).

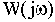
К содержанию


Содержание раздела

---

---